1. 偶数次LPFの振幅と遅延周波数特性(4次の例)
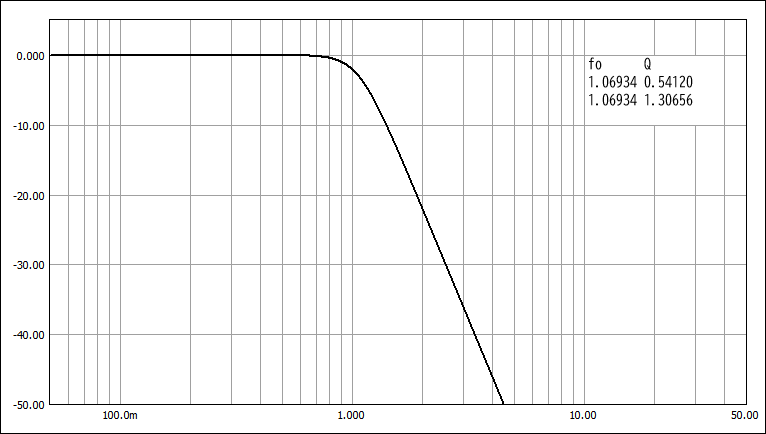
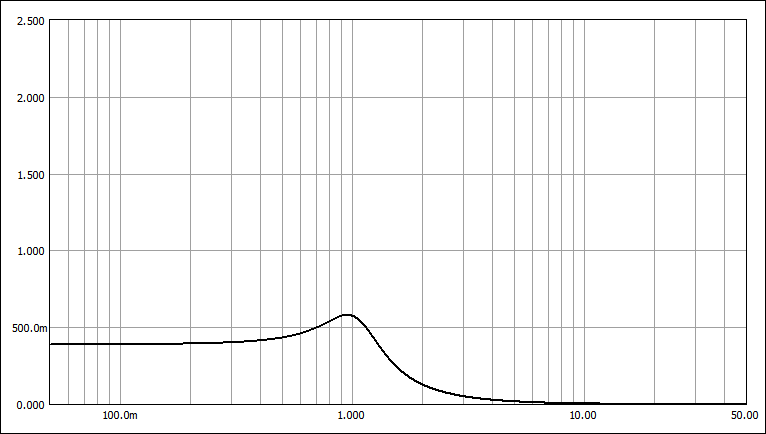
W-W特性 (Ws=3.382)
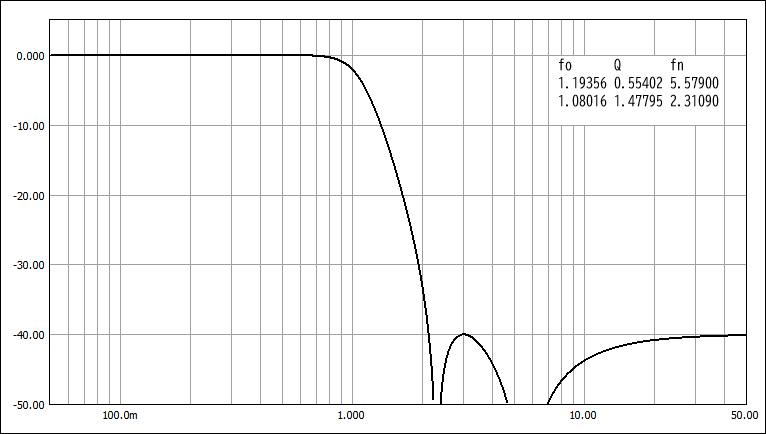
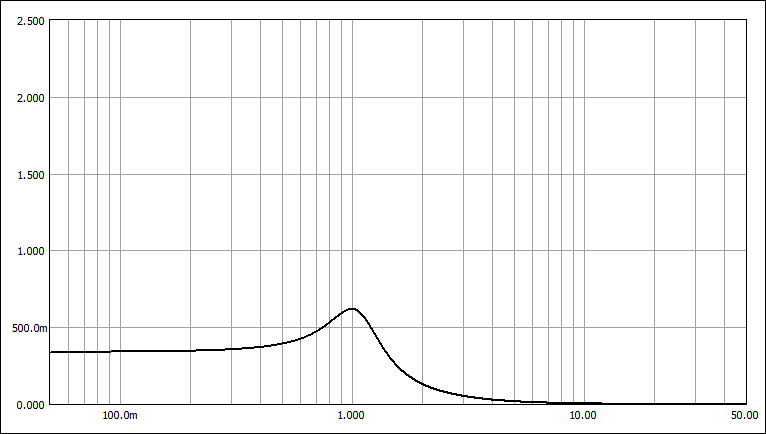
W-T特性 (Ws=2.135)
T-W特性 (Ws=2.135)
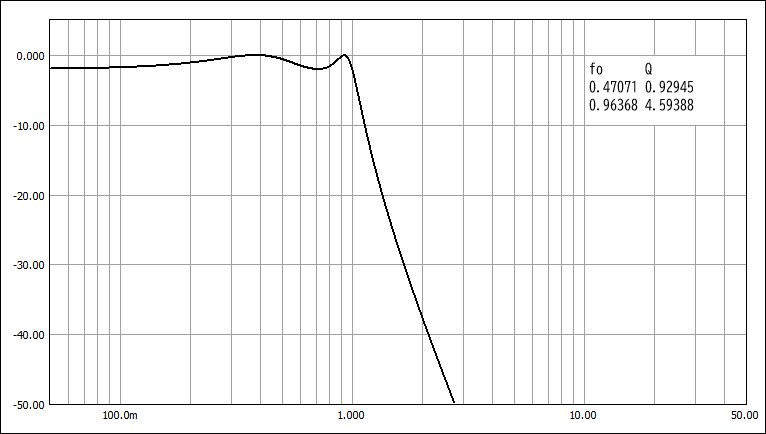
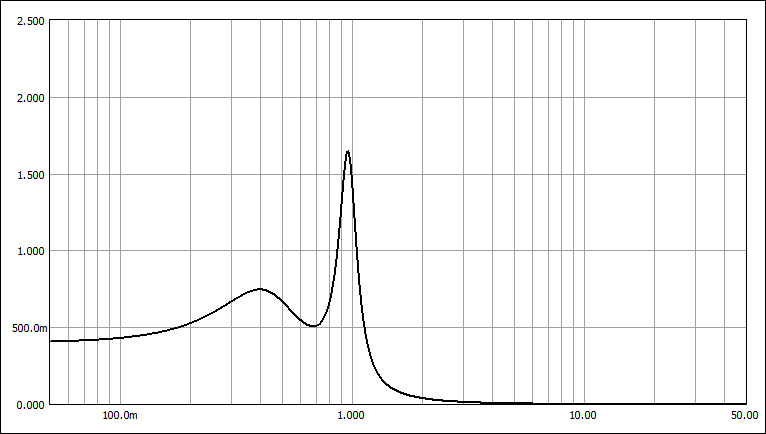
T-T特性 (Ws=1.408)
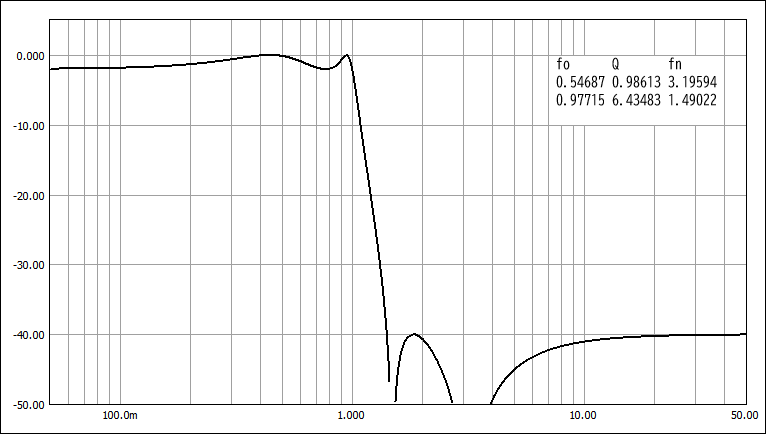
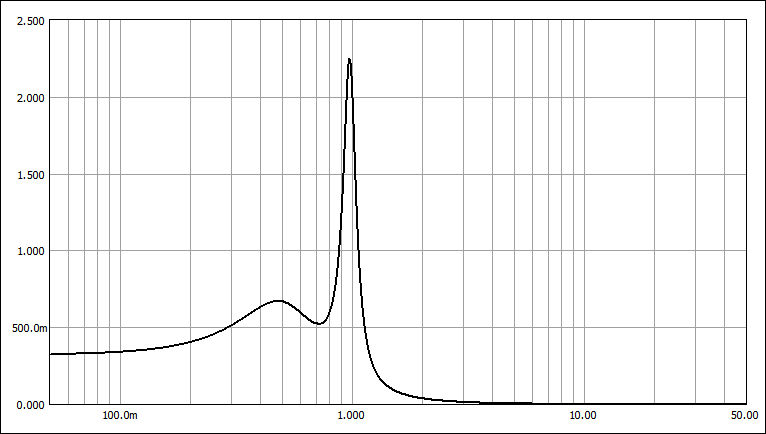
2. 奇数次LPFの振幅と遅延周波数特性(5次の例)
W-W特性 (Ws=2.650)
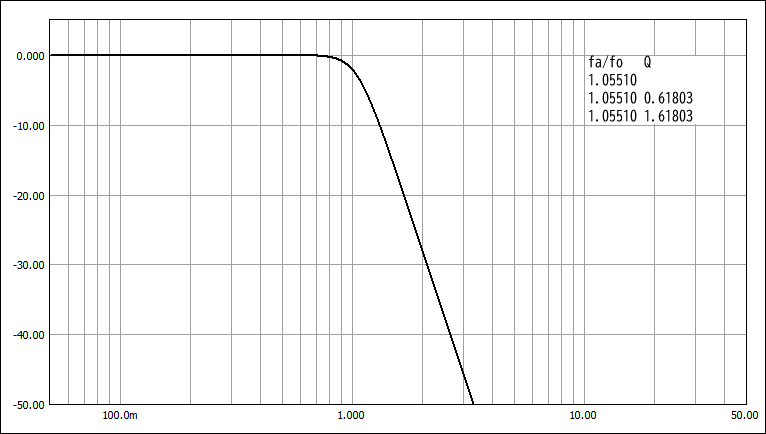
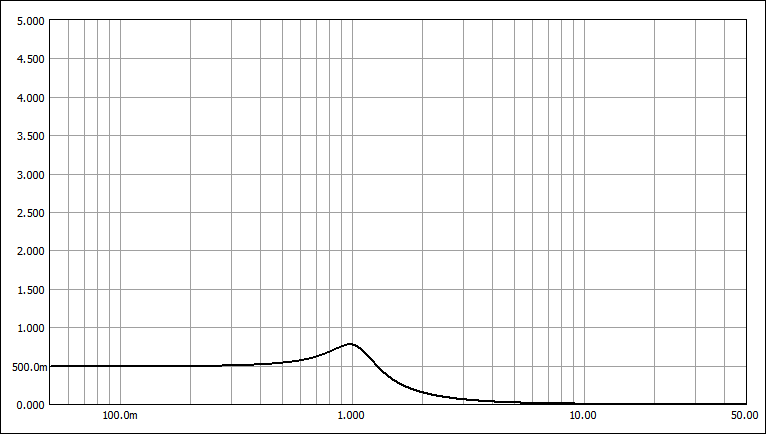
W-T特性 (Ws=1.686)
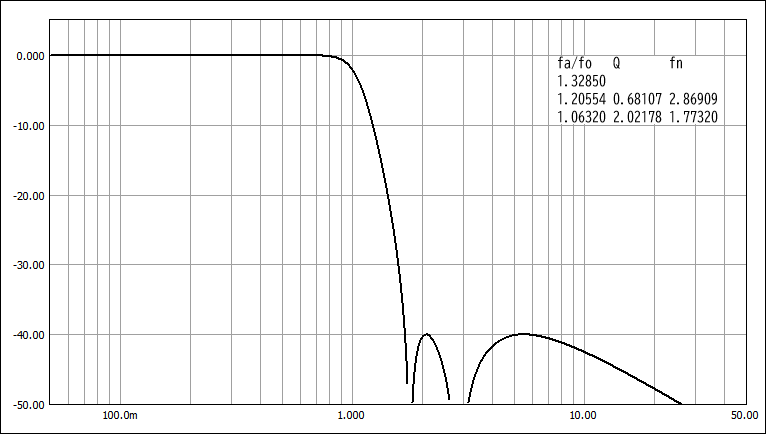
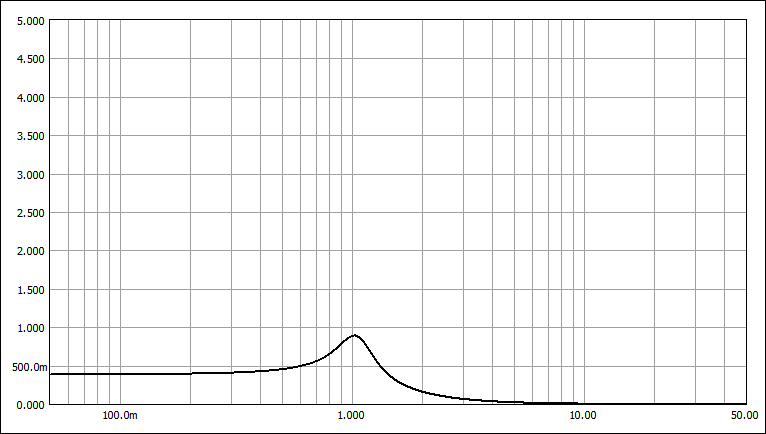
T-W特性 (Ws=1.686)
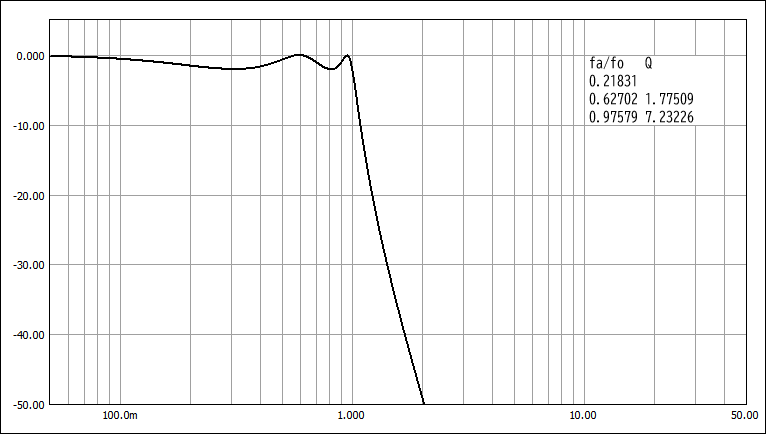
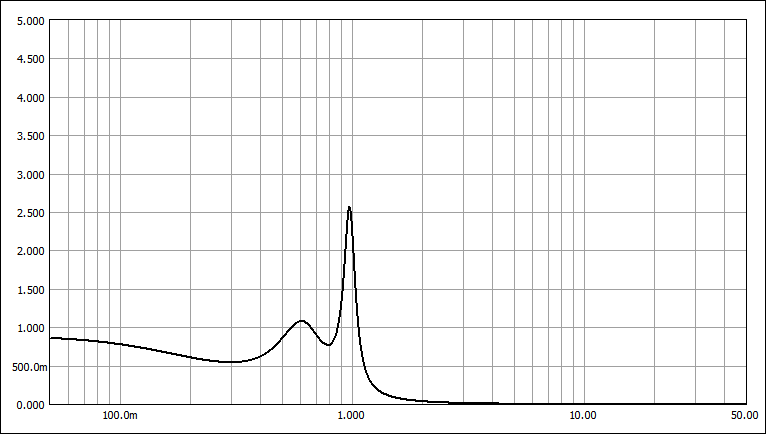
T-T特性 (Ws=1.168)
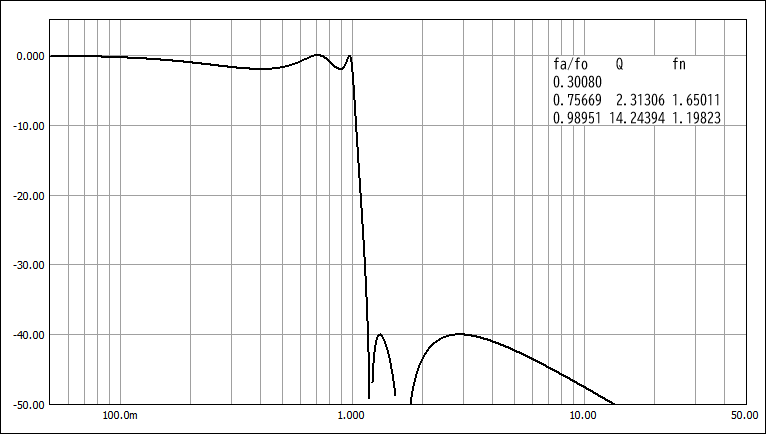
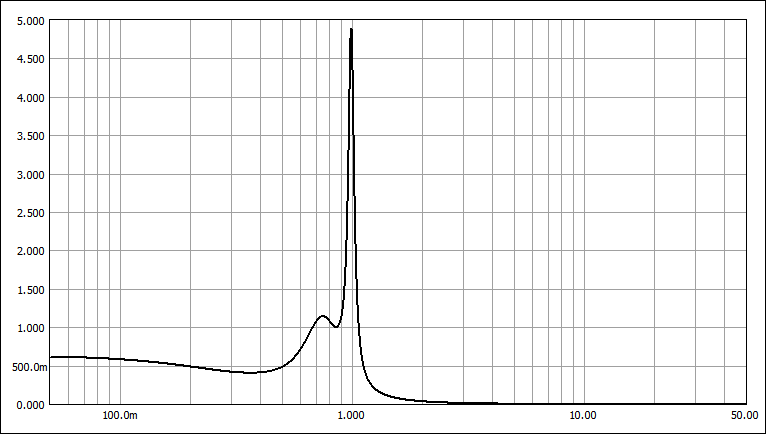
3. 遮断特性の特徴
W-W特性:遮断特性が緩やかで遅延特性も単調変化。遮断域の傾斜はLPFの場合 -N*6.02dB/Oct (N=次数)
W-T特性:遮断特性がやや急峻、通過域の遅延特性は単調変化。
T-W特性:遮断係数(Ws)はW-T特性と同等だが遷移域の減衰量が大きい。通過域の遅延特性にリップルを生じる。
T-T特性:遮断特性が急峻。通過域の遅延特性にリップルを生じ遅延時間も大きい。
W-W, W-T=T-W, T-Tの順に少ない次数で遮断係数(Ws)を実現できるが高いQが必要になる。
高Qの区間には高精度、低温度係数の部品が必要になります。
4. フィルタ次数の偶奇による違いについて
阻止域チェビシェフ特性の偶数次のフィルタは阻止域の端部(HPFでは0Hz)で減衰量が有限(As)になります。
LPF,HPFでは奇数次に上げるためのコストは小さいので奇数次にしたほうが有利です。
LCフィルタの場合は偶数次の通過域チェビシェフフィルタは整合トランスが必要になるため実用的ではありません。
5. 遅延特性について
通過域チェビシェフ特性の場合は通過域の遅延特性にリップルを生じます。
遅延特性を平坦にしたい場合は通過域ワグナー特性フィルタに全域通過フィルタを追加して補正可能です。
原理上周波数∞での遅延はゼロなのでHPFでは遅延特性を平坦にできません。
6. 遅延特性の補償
5次のW-T特性LPFに全域通過(APF)2段を追加して手作業で遅延特性を平坦化した例
遅延特性
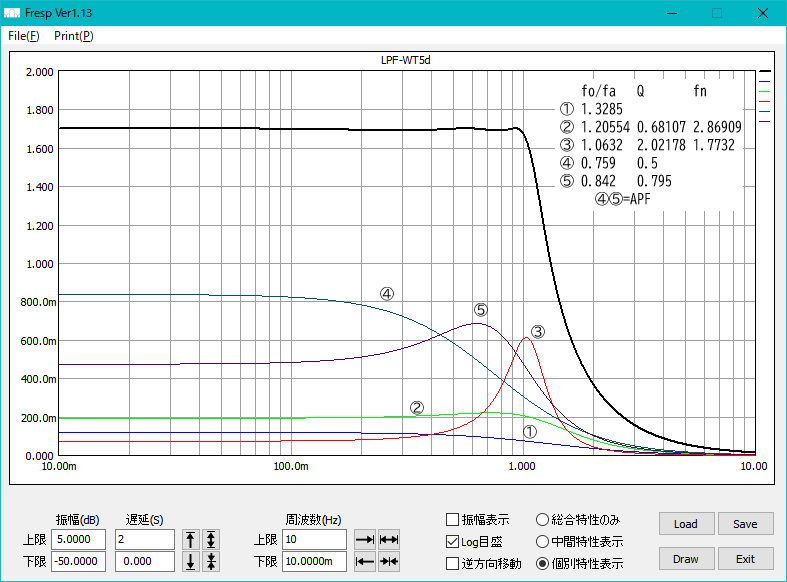
振幅特性
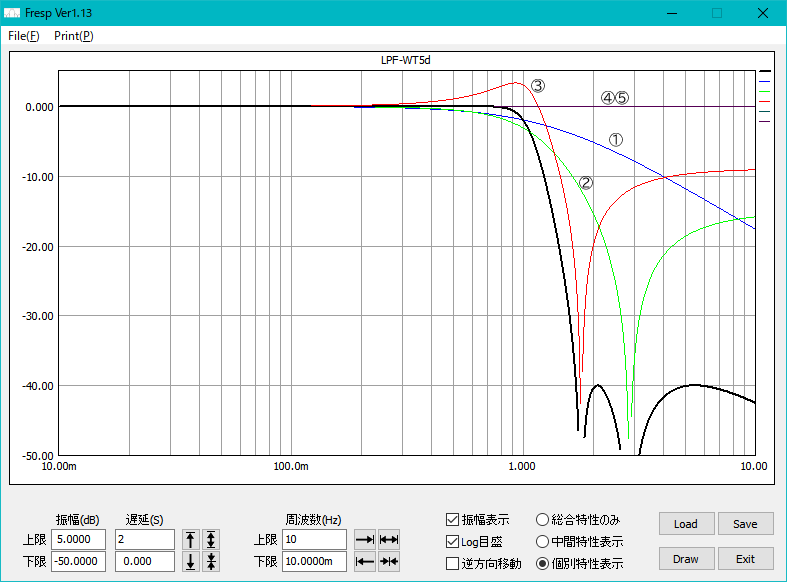
伝達関数CSVファイル:LPF-WT5d.csv
|